Je souhaite avoir des informations sur la notion de puissance en mathématiques

Publiée par :

Le 18/02/2024 à 21h53 121 vues

Question d'origine :

Mon guichet préféré, bonsoir.
Deux questions à propos de la notion mathématique de « puissance d'un point par rapport à un cercle » :
0) pourquoi le terme « puissance », qui a du sens en mécanique et particulièrement en énergétique, mais que je ne comprends pas ici ;
1) historiquement, pourquoi cette notion est apparue et à quoi peut-elle servir ?

Réponse du Guichet

Sciences8 - Département : Sciences et Techniques

Le 20/02/2024 à 17h45

La puissance d'un point par rapport à un cercle traduit la distance relative d'un point à un cercle.

Si cette puissance est positive, le point est à l'extérieur du cercle. Si elle est négative, le point est à l'intérieur du cercle. Enfin, si la puissance est nulle, le point est sur le cercle.

C'est le mathématicien grec Euclide qui a introduit les premières mentions de cette notion dès le IIIe siècle avant JC.

Bonjour,

Vous vous interrogez sur la notion géométrique de Puissance d'un point par rapport à un cercle.

Théorème et définition

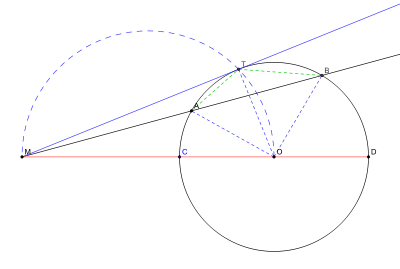
En géométrie euclidienne du plan, la puissance d'un point M par rapport à un cercle de centre O et de rayon R est un nombre qui indique la position de M par rapport à ce cercle.

Soient M un point, Γ un cercle de centre O et de rayon R et (d) une droite orientée passant par M et rencontrant le cercle en A et B. Alors le produit MA × MB des mesures algébriques de MA et MB est indépendant de la droite orientée choisie et vaut MO² – R².

La puissance du point M par rapport au cercle Γ est notée P_Γ(M).

Ainsi, la puissance est P_Γ (M) = OM² – R².

Source: Puissance d’un point par rapport à un cercle (Wikipedia)

Pourquoi utiliser le terme Puissance?

La puissance d’un point par rapport à un cercle correspond à la mesure de la proximité de ce point par rapport au cercle.

Cette terminologie de Puissance est utilisée pour décrire la relation de force ou l’influence du point par rapport au cercle.

En fonction de sa localisation, le point agit sur le cercle ou est influencé par le cercle. Ainsi, la puissance est:

Positive si le point est à l’extérieur du cercle: le point exerce une influence sur le cercle
Négative si le point est à l’intérieur du cercle: le cercle exerce une influence sur le point
Nulle si le point est sur le cercle: le point et le cercle ont une influence équilibré

Historique de la notion

La notion de Puissance d’un point par rapport à un cercle a une histoire dans la géométrie qui remonte à l’antiquité.

Dès le livre III des Éléments, Euclide mathématicien grec du IIIe siècle avant Jésus Christ, traite des propriétés des cercles et de leurs tangentes.

Un autre mathématicien grec, Apollonius de Perga développe cette notion de puissance du point dans son traité Les coniques, avec des études détaillées portant sur les cercles, ellipses, hyperboles et paraboles.

Cette notion continue d’être étudiée au fil des siècles. L’allemand Jacob Steiner pose la première définition de la puissance d’un point dans son livre Quelques observations géométriques. Il a contribué de manière importante aux théories de géométrie projective, ouvrant toujours plus la voie aux développements de la géométrie moderne.

[Cependant]

Parler de «puissance d’un point par rapport à un cercle» peut paraître de nos jours suranné. La notion a le parfum oublié des vieux livres de géométrie. En tout cas, elle figurait en bonne place dans les manuels de seconde des années soixante.

Source: Tangente

Intérêt de la notion

La puissance d’un point simplifie considérablement les recherches de lieux géométriques et conduit à la notion de dualité, ouvrant ainsi de vastes et nouvelles perspectives.

Source: Tangente

Cette notion trouve de nombreuses applications pour la résolution de problèmes géométriques avec des applications pratiques : applications en physique (optique géométrique, trajectoire de particules…), applications en géométrie projective (problème de construction) ou encore pour le calcul de positions relatives (cartographie et topographie).

Géométriquement votre.