La voix du cavalier.

Bonjour,

Ce problème mathématique est aussi appelé problème du cavalier ou cavalier d’Euler ou encore polygraphie du cavalier.

(Source : Problème du cavalier / Wikipédia)


Les règles sont simples : un cavalier doit parcourir toutes les cases d'un échiquier sans revenir sur une case déjà visitée. […]

La plus ancienne description connue du problème du cavalier remonte au milieu du IXe siècle dans un manuscrit arabe. Deux joueurs d'échec y exposaient chacun leur solution, l'une était un parcours fermé (la cavalier revient à la case de départ).

Depuis, de nombreux mathématiciens s'y sont intéressés de près. C'est le cas par exemple du mathématicien suisse Leonhard Euler (1707-1783) qui publie un des premiers traités sur la question en 1766. C'est pourquoi ce problème est parfois appelé "cavalier d'Euler". A cette époque, l’académie des sciences de Berlin (où Euler était directeur du département de mathématiques) avait jugé le problème suffisamment important pour proposer un prix conséquent pour le meilleur mémoire sur le sujet. […]

Une question sérieuse

Le problème du cavalier est bien plus qu'un simple amusement. Il est relié à un champ extrêmement important et fécond des mathématiques appelé "théorie de graphes" , un domaine qui a des retombées très concrètes sur notre vie de tous les jours. Les graphes modélisent de nombreuses situations où interviennent des objets en interaction : connexions routières, ferroviaires ou aériennes, plan d'une ville et de ses rues en sens unique, liens entre les composants d'un circuit électronique. L'ensemble des outils mathématiques mis au point dans ce domaine permettent de démontrer facilement les propriétés d'un graphe et d'en déduire des méthodes de résolution : quel est le plus court chemin pour se rendre d'une ville à une autre ? Comment minimiser la longueur totale des connexions d'un circuit ? Peut-on mettre une rue en sens unique sans rendre impossible la circulation en ville ?

(Source : Le cavalier polygraphe / Procrastin)


Il faut savoir qu’il n’existe pas une solution à ce problème mais des milliards suivant la taille de l’échiquier. De plus, il est possible de résoudre cette énigme de deux façons différentes : en circuit ouvert (le cavalier fait le tour de l’échiquier en passant une seule fois sur une case) ou en circuit fermé (le cavalier revient à son point de départ à la fin du tour) ; ce qui change la donne quant aux solutions.

Plusieurs ressources vous expliquent comment trouver les solutions à ce problème :
• Problème du cavalier
• Les 13267364410532 circuits fermés du cavalier / La Recherche
• Une invitation à la théorie des graphes / Groupe pour l’Initiative et la Culture Scientifique
• Le problème du cavalier d’Euler / Comment ça marche ,

Voici une des solutions possibles :


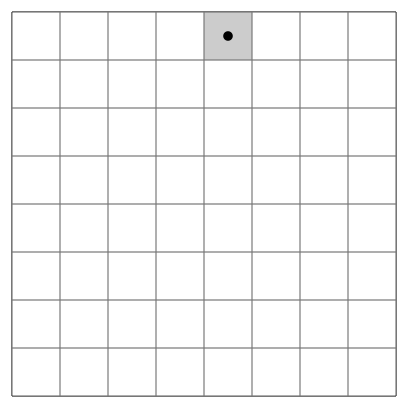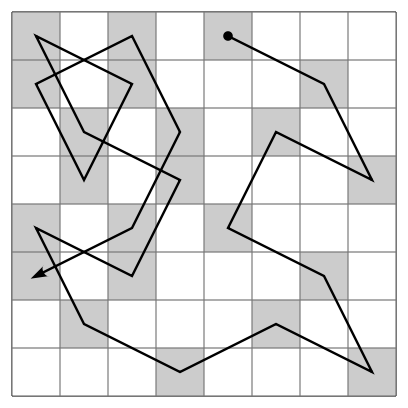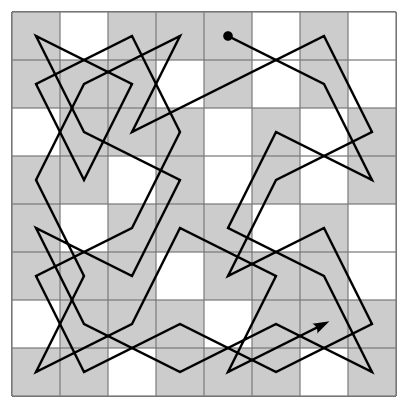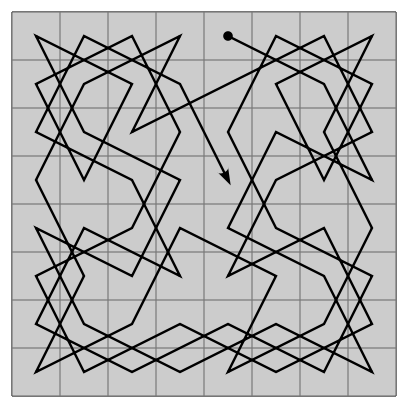
By Ilmari Karonen [CC0], via Wikimedia Commons


L’ouvrage Euler : les mathématiques et la vie vous donnera tous les détails sur la méthode utilisée par Euler pour résoudre la polygraphie du cavalier.


En effet, il semble que la marche du cavalier serve dans le décryptage des messages codés par transposition.

(Source : Chiffres de transposition / Apprendre en ligne)



Enfin, notons que Georges Pérec a construit la structure de son roman La Vie mode d’emploi suivant le cheminement du cavalier :

Il aurait été fastidieux de décrire l'immeuble étage par étage et appartement par appartement. Mais la succession des chapitres ne pouvait pas pour autant être laissée au seul hasard. J'ai donc décidé d'appliquer un principe dérivé d'un vieux problème bien connu des amateurs d'échecs : la polygraphie du cavalier (cf. François Le Lionnais, Dictionnaire des Échecs, PUF, 1974, pp. 304-305) ; il s'agit de faire parcourir à un cheval les 64 cases d'un échiquier sans jamais s'arrêter plus d'une fois sur la même case. Il existe des milliers de solutions dont certaines, telle celle d'Euler, forment de surcroît des carrés magiques. Dans le cas particulier de La Vie mode d'emploi, il fallait trouver une solution pour un échiquier de 10 x 10. J'y suis parvenu par tâtonnements, d'une manière plutôt miraculeuse. La division du livre en six parties provient du même principe : chaque fois que le cheval est passé par les quatre bords du carré, commence une nouvelle partie.
On remarquera cependant que le livre n'a pas 100 chapitres, mais 99. La petite fille de la page 295 et de la page 394 en est seule responsable.

(Source : La « polygraphie » du cavalier / BnF)



Bonne journée